Error Calculator: Percentage, Absolute, Relative

This error calculator allows you to calculate Absolute, Relative, and Percentage errors with just one click. You can also easily copy the results along with the formulas used and apply them wherever you need.

Human error is a real and unavoidable part of measurement. There is almost always a difference between the true value and the measured value. This difference can result from various factors such as limitations of the measuring instrument, environmental conditions, personal bias or misreading, and flaws in the observation process.

That is why it is important to understand absolute error, relative error, and percentage error. You can easily calculate these errors with the A Calculator Online‘s error calculator.

You might also like to use:

• Compound Interest Calculator: Daily to Yearly Compounding
• BMI Calculator for All Units
• Numerology Name Number Calculator (Get Quick Answer)
• Discount Calculator: % Off, Double, Triple

Absolute Error:

Absolute error is simply the difference between the true value and the measured value. It’s like if a true value was 100, but the measured value is 98, it means the absolute error is 2.

Formula to calculate absolute error:

Absolute Error = |Measured Value - True Value|

Now, let’s understand with a real-world problem.

For instance, you’re an engineer testing the strength of a new metal rod. The true breaking force (let’s say the standard value) for the material is 5000 Newtons, but during testing, you got the measured value as 4820 Newtons.

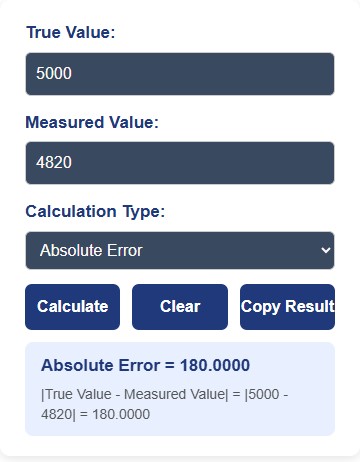
To calculate the absolute error, you simply subtract the measured value from the true value:

Absolute Error = |5000 - 4820| = 180 Newtons

This means there is an absolute error of 180 Newtons.

If you’re not an engineer, maybe a student, you might be wondering why this matters. Finding absolute error helps you understand whether the measurement is acceptable or if the testing method or equipment needs calibration.

Something to consider is that the absolute error is always positive. That’s why it appears inside the modulus (| |), which means even a negative value will be converted to a positive one.

Relative error:

Relative error is the ratio of the absolute error to the true value.

Formula to calculate relative error:

Relative Error = Absolute Error / True Value

Let’s say the true value is 100, and the measured value is 98. So, the absolute error is 2.

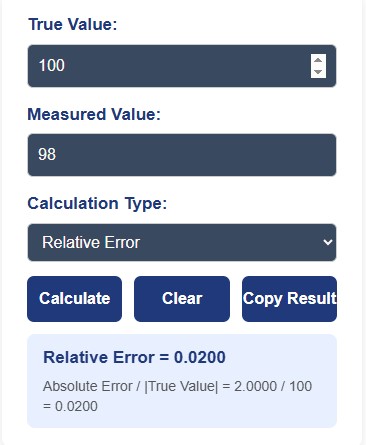
Now, we can find the relative error as:

Relative Error = Absolute Error / True Value = 2 / 100 = 0.02

You might be wondering, why is it important to calculate the relative error?

Let’s understand this with an example.

Suppose someone measured the distance between two buildings that are 10 km apart and found an absolute error of 100 cm. The same person also measured the height of a building that is 20 feet tall and got an absolute error of 10 cm.

Now, both errors are in centimeters, but let’s calculate the relative errors for both measurements:

Distance between buildings:

True Value = 10 km = 1,000,000 cm

Absolute Error = 100 cm

Relative Error = Absolute Error / True Value

               = 100 / 1,000,000
               = 0.0001

Height of building:

True Value = 20 feet = 609.6 cm

Absolute Error = 10 cm

Relative Error = Absolute Error / True Value

               = 10 / 609.6
               ≈ 0.0164

Now, both absolute errors were in centimeters, so apparently both seem accurate. But with the help of relative error, we can now see that the error in building height was many times greater than the other one.

And you might need to reconsider your measurement.

Percent Error:

The percentage error is simply the relative error expressed as a percentage. You might already know that to find a percentage, you just multiply it by 100.

So, the formula will look like:

Formula to calculate relative error:

Percentage Error = (Absolute Error / True Value) × 100%

Now, using the previous example, let’s understand why percentage matters. When we look at the relative errors in the previous examples, the errors are 0.0001 and 0.0164, respectively.

Both values don’t give a clear understanding of how much the error is, but when we find the percentage, it becomes obvious that the first value is almost the same as the true value, but the second example has a 1.64% error.

Distance between buildings:

Percentage Error = (100 / 1,000,000) × 100% = 0.01%

Height of building:

Percentage Error = (10 / 609.6) × 100% ≈ 1.64%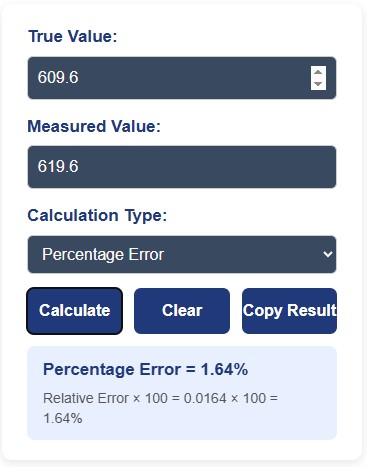

Approximation Error:

The other example can be an approximation error. In maths, we often round off values. For instance, we write 5.345 as 5.35. It has an approximation error, and we can see how much it is with a real-time example.

If you have ever read maths, you might know π. The value of π is 3.1416, but we use it as 3.14. The absolute error is:

Absolute Error = |3.1416 - 3.14| = 0.0016

The relative error is:

Relative Error = Absolute Error / True Value

               = 0.0016 / 3.1416 ≈ 0.00051

And the percentage error is:

Percentage Error = Relative Error × 100%

                 ≈ 0.051%

It means the value of π we often use comes with a percentage error of 0.051%.

Negative Percentage Error:

As we discussed earlier, we use positive values to find absolute error. But the question is, do negative percentage errors exist, and do they matter?

Yes, they do exist and matter in cases where it is important to show whether the measured values were greater or smaller than the true value.

Negative percentage errors indicate that the measured or approximate value is less than the true value, while positive percentage errors show that the measured value is greater.

Example:

Imagine a pharmaceutical company measuring the concentration of an active ingredient in a medication. The true concentration should be 50 mg/mL. If a test shows a concentration of 48 mg/mL, the percentage error is:

Percentage Error = ((48 - 50) / 50) × 100% = (-2 / 50) × 100% = -4%

This negative percentage error indicates the concentration is 4% less than the intended amount, which could affect the medication’s effectiveness and patient safety.

On the other hand, if the measured concentration was 52 mg/mL:

Percentage Error = ((52 - 50) / 50) × 100% = (2 / 50) × 100% = +4%

This positive percentage error shows the concentration is 4% higher than expected, which might also be critical for dosage safety.

But both positive and negative percentage errors can have different effects and different considerations to figure out where the problem originated.

Therefore, showing the sign of the percentage error is important in some cases. But mostly, percentage calculators give positive values.